在高能物理与量子场论中,费曼积分的解析计算长期面临多圈复杂拓扑结构、多标度计算困难等挑战。传统方法如Mellin-Barnes积分或微分方程技术虽有效,但在处理高圈图时仍存在计算量爆炸的瓶颈。近期,理论物理团队在量子场论精细计算方面取得新进展,为组合几何与量子场论的数学物理交叉研究提供了新范式,在多圈费曼积分的解析计算新方法的探索上取得系列创新成果,发表在量子场论与高能物理领域顶级期刊《Physical Review D》与《Journal of High Energy Physics》。
1. 费曼积分超几何函数表示的高斯关系
相关工作“Gauss Relations in Feynman Integrals”发表在《Physical Review D》(2025, 111, 016015),冯太傅教授为第一兼通讯作者,张海斌教授为共同通讯作者。
将费曼积分嵌入到格拉斯曼流形中,可以将费曼积分写成广义超几何函数的有限线性组合。在该论文中,提出了一种通用方法来获取这些广义超几何函数之间的三类高斯关系。通过逆高斯关系,费曼积分的超几何表达式从一个连通区域延拓到另一个区域,然后再通过高斯库默关系延拓到整个定义域。通过高斯比邻关系,可以得到费曼积分在时空维数D = 4邻域的洛朗级数。以单圈有质量自能图与双圈无质量三角图为例,验证了该方法的可行性与数学表示的解析性。该论文通过超几何函数的拓展高斯关系,创新性地来完成相应超几何解析表达式的解析延拓。
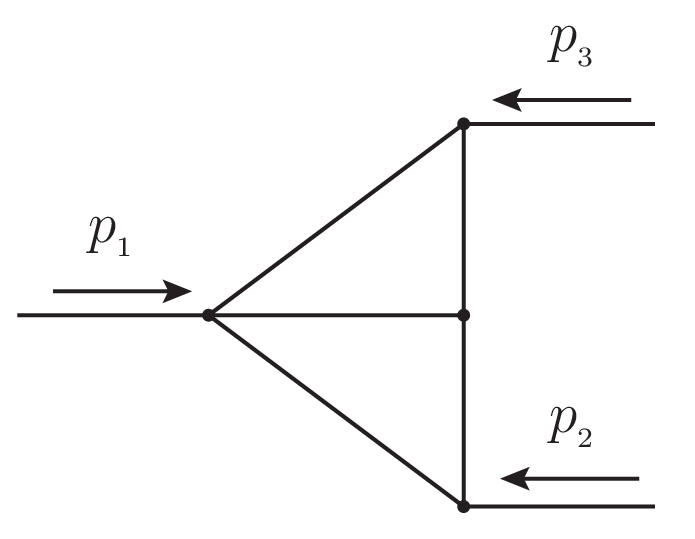
图1 双圈三角费曼图
2. 四圈真空费曼积分的GKZ超几何表示
相关工作“GKZ hypergeometric systems of thefour-loop vacuum Feynman integrals”发表在《Journal of High Energy Physics》(2025, 03, 013),张海斌教授为第一兼通讯作者,冯太傅教授为共同通讯作者。
该论文应用Melin-Barnes表示及Miller变换,构建了五个拓扑结构的带质量四圈真空费曼图的GKZ超几何偏微分方程组的计算框架,可以得到在零点及无穷远点邻域的四圈真空费曼积分的超几何解析解。其在非空收敛域下的解析解可以组成一个基础解系,四圈真空费曼积分可以表示为基础解系的线性组合。通过程序验证,在通用计算机里利用GKZ解析结果的计算效率将远高于数值程序FIESTA。该论文首次将GKZ超几何表示应用于四圈积分,突破了传统方法在高圈图解析计算中的瓶颈。
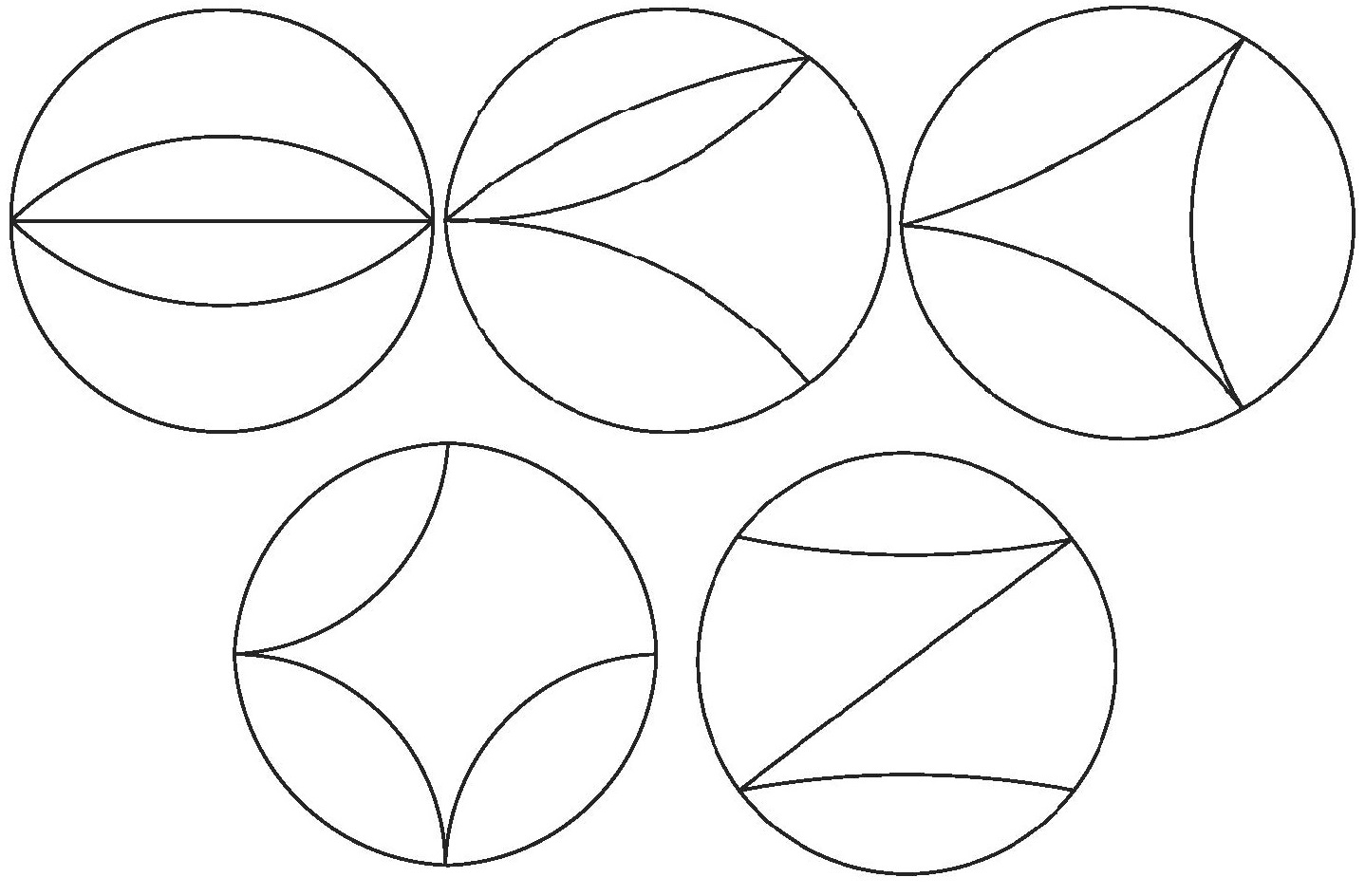
图2 五个拓扑结构的四圈真空费曼图
上述工作依托于河北省量子场论精细计算与应用重点实验室、河北省计算物理基础学科研究中心等研究平台,得到了国家自然科学基金重点项目、面上项目,河北省杰出青年科学基金项目,河北省青年拔尖人才支持计划项目及河北大学青年拔尖人才培养项目等基金项目资助。
论文链接:
https://doi.org/10.1103/PhysRevD.111.016015
https://doi.org/10.1007/JHEP03(2025)013

